The algebraic structure of functions, illustrated using React components

All right.

The algebraic structure of Functions Illustrated using React components.

I'm just gonna come out and say it.

This is possibly the worst conference talk title ever.

it's not exactly click bait is it, but.

The thing is, I am excited to tell you about algebraic structures because they will change the way you think about code forever in a good way.

And they work no matter what programming language you are working in.

Now, some of you think I'm exaggerating, but let me ask you this.

How many of you have ever felt out of your depth in your job?

Wow, that's more than I was expecting in a room full of Web developers.

I have too.

So back in July of 2020, I was coming to the end of my first year at Atlassian and it was annual review time.

And normally for me that's not much of an issue.

But the thing is, Atlassian had hired me as a full stack developer.

And again, that's not normally an issue for me either.

I've done plenty of Node and other kind of PHP, Pearl work, but the trouble is our team works on Jira.

And I dunno if but Jira is a kind of heinously, complex Java application and my Java knowledge at the time was about 12 years out of date.

So there I was madly trying to learn things like Spring, Maven, Spring Boot auto wiring, property tests in J Unit, and it just wasn't happening fast enough.

I needed some way to demonstrate that I could provide value to the team on the backend.

And so I'm sitting at home.

I work remotely.

So I was in my home office and it's middle of winter and I'm literally sweating.

And then something happened.

Cuz I'm a full stack developer.

I dunno whether it was out of obligation or whether it's just cause they wanted more, approvals quicker, but the backend developers started putting me on their pull requests to get some reviews.

And it just so happens that this part of Jira that we were working on, it had been ported from Scala and because of that it was using a bunch of data structures like option and task and either and a metric crap ton of Java streams.

And so because I understand the rules of algebraic structures, I was able to look at these and go, that there, that should obey the func to composition law.

And this other thing here.

if we rearrange these methods, then we should get a performance improvement.

And so I start typing these away on my, my, my PR.

And to my great surprise, the backend developers, not only do they implement the changes, they say thank you, and so that's pretty good.

But then the next week I'm working away and I'm on Slack and one of my colleagues pops up and says, Hey, would you mind jumping on a Zoom call?

I wanna do some pair programming because I'm really struggling with these sort of tasks and options, and I'm getting muddled up and you seem to know what you're doing.

So we jump on a pair programming session and because I know what my colleague's trying to do, and I know the way algebraic structures work, it's like seeing a hole in a jigsaw puzzle.

And so I would say, there should be a method somewhere in the documentation that has a type signature like this does this kind of thing.

And maybe it's called fold, maybe it's called reduce.

We don't know.

Let's have a look.

And lo and behold, there it is.

And because of this, um, my colleague's happy, I'm starting to show some, value to my team.

And the same thing happened again a week later with yet another backend developer.

And so because I understood the laws and the rules of algebraic structures, I was able to deliver some value to my team on the backend in a programming language where my knowledge was 12 years outta date.

Now this is a React track, and so you're probably thinking, I don't work with Java code ported from Scala, and that's totally fair.

That's why today I want to talk to you about an instance of algebraic structures that you find everywhere, especially in JavaScript, and that is functions.

And now by this point, some of you might be wondering, what the heck is an algebraic structure anyway?

So in case you're wondering, a algebraic structure is a bit like a design pattern.

Some of you might be familiar with those from object oriented programming.

And a design pattern is a description of a pattern that people have seen come up over and over again in code, and they've codified it so that people can reuse it.

Now, algebraic structures are similar, but they have a mathematical definition rather than a descriptive one.

And this mathematical definition consists of some sort of data structure.

Some operations that we can do on that data structure, including specific type signatures they have to follow, and then some laws or rules that they have to obey.

Now, all that may sound quite complicated, but what they are isn't nearly as interesting as what we can do with them.

So we're gonna focus on that today.

We're gonna focus on the definitions and, the laws and stuff.

So we're gonna look at four structures today.

They are Functor, Profunctor,, applicative functor, and Monad.

Now that may sound like gobbledygook.

The only reason I'm giving you these names is because if you wanna learn more, that's what you have to go searching for.

Otherwise, they're completely useless.

So let's press on and let's have a look at some of these.

But the first thing we need to understand is that functions can be data structures.

Now, normally we're used to thinking of functions as verbs.

They're the things that do stuff to data.

But the thing is, functions can be data structures in their own right, and it's quite easy to put data into a function and we can get it out again.

We just create something called a thunk.

Now, a thunk is a function that takes no Input, but returns a value.

And to create a thunk, we just stick some parentheses and a fat arrow in front of any expression.

And so it's quite easy to create thunks.

Now, the first algebraic structure we're gonna look at is called functor.

and for functor, we have to define an operation called map.

Now, I'm hoping that all of you are already familiar with a data structure that has this operation, and that is the humble array.

Now, I'm gonna draw a picture of an array, and it looks like this.

And so I'm representing this array as a rectangle, and this particular rectangle holds things of type A.

Now A could be anything, it doesn't really matter.

And now I'm gonna draw a picture of a function.

It takes something of type A and transforms it into something of type B.

Now, for the moment, we are gonna pretend that all JavaScript functions take just one input parameter.

I know that's not true, but that's the way mathematicians think about functions, and we'll come back to how we handle multiple input parameters later on.

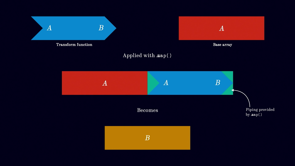
So here's a picture of how the map operation works for arrays.

We have our base array and we have our transform function and map applies that transform function to our base array, and we get back a new array of type B.

Now notice how A and B have the same shape.

The rule for functors is that if we, we start with a rectangle, we have to get a rectangle back at the end.

So if we start with an array, we have to get an array back at the end with the same number of elements.

We're talking about functions today, not arrays.

So what happens if we stick a function in that spot on the right?

Can we apply that transform function to the value in the base function and get back something of the same shape?

So for it to work the same as a raise, we know that the resulting shape has to contain type B, so it would look something like this.

Now how do we make that work?

when we look at it as a picture, the answer is obvious.

we create a function, it takes that output, A from the base function, and it pipes it into transform function.

And then we've got something that's in the same shape.

Now those question marks, though, they're a little bit odd.

Now, I put them there because we're just talking about thunks and thunks don't care what the input is.

We just know we get something back of Type A.

But with a little bit of rearranging, we can rewrite all these letters and we've got a more generalized picture of map for functions.

And so the more traditional way to describe map looks like this.

We've got a base function.

It goes from A to B.

We've got a transform function that goes from B to C, and we get a function at the end that goes from A to C.

Now, pictures are all very pretty.

How do we do that in code?

Now, one way to write it is like this.

So a map function, it takes two parameters.

Both of them are functions.

So the first one is a transform function.

Second one is a base function, and it returns a new function that takes some input, passes it to the base func.

And then the result of that to transform func and then returns the result.

Pretty straightforward.

Wait a second.

I said just a moment ago, we were gonna pretend that all functions take just one Input parameter.

So what we're gonna do is we're gonna curry this function.

That means instead of taking two arguments, we're gonna take one argument and we're gonna return a function that expects the second argument and then returns what we would've or expected.

It sounds a lot more complicated than is if we use just a bit of fat arrow shorthand, we get a function that takes a parameter, returns a function that takes another parameter, and then returns the main function.

Now, if you're paying careful attention, you might be thinking, that looks suspiciously like function composition, and you'd be absolutely right.

It is in fact function composition.

For functions, functor mapping and function, composition, try saying that fast are, one and the same thing.

So how do we use this function then?

I'm gonna assume you've all seen or done some kind of function composition before, so I'm not gonna bore you with hello world type code.

Instead, what we're gonna do is we're gonna have to think about React components because React components just happen to be functions, or at least they can be.

So what's the type of a React component?

How would it look like in our little diagram from earlier?

if we simplify things a little bit, we are just focusing on components, that are function components.

A React component is a function that takes a prop and returns a node.

And a node just means anything that React can render.

So what happens if we put a React component up in the top right of that diagram we had before where our base function went?

What happens to the types?

Now if we substitute all the letters through?

So anywhere we had an A, we write props, everything where we had a B, we write node.

we've done that, our, transform function, it takes a node, but it can still return anything it wants.

We've still got that weirdo C hanging around.

But I want you to consider with me, what if we change that C to node?

Try mentally substituting that in there.

What do we get out at the end?

what we get way down at the bottom there is something that takes props and returns a node, which is the same type as a component.

So in other words, what map does, it lets us take a function that mucks around with nodes.

Takes a node, returns node, and with map we lift it up into the world of components.

At least that's one way to think about it.

So when would you ever want that kind of thing?

what's this for?

suppose just for the sake of example, you work for a company that's large enough to have multiple products and its own design system, like, I don't know, say Atlassian, but suppose also that you work on just one product.

And it has its own sort of patterns and unique ways of doing things.

They're variations on what the design system provides, and they're a little bit different.

In that case, what we could do is we could write a bunch of functions that modify nodes or elements, and then we could use map to create components that we can use for our purposes wherever we want.

for example, let's, have a look at some code.

We're gonna import some things from Atlas Kit, which is Atlassian's design System.

And it's, openly available so you can use it if you want to.

so we're gonna import a button and a lozenge, which is like a, status kind of thing, and a premium icon, which is like the, sparkle emoji if you've ever seen that.

And so what we're gonna do is we're gonna create a function now, it puts that shiny premium icon after some element or node.

And then what we're gonna do is we're gonna take our map function, we're gonna use that to create new components.

So we run that same append icon function.

We map it over button and we map it over lozenge.

And we get a premium button and a premium lozenge.

Now see how we've got those double parentheses?

That's just cause we're using curried functions and we pass I parameters just by calling the return function.

Hope that's not confusing anyone.

Now we can use those components anywhere we want in our application, and here they are with their sparkly icons on the end.

Now that's not super useful.

What else could we do?

let's look at something that's maybe a little bit more useful here.

We could put a label in front of something.

So I've got this prepend status and it puts status in front of any node we pass in.

And so I could map that over a badge element or a lozenge element, and we get a status badge and a status lozenge, and then we can use that in our application.

And notice how in that second one there, I've passed in a prop.

It's an appearance, success prop, which makes that green done thing, that done sort of lozenge go green.

I didn't have to do any wiring to make that happen.

It just passed through because that's how compose works.

Other thing we do is we could wrap some elements with some other element like this one that wraps 'em with a span.

It has a navy border applied.

So if we do that, we get a dignified button and a dignified text field, and then we use that in an application and we get, that navy border around things.

Now we can do any combination of those so we can use functor and the power of map to modify existing components and create new reusable components.

What if going back, thinking back to those diagrams we went the other way?

That is, could we change the input to a function instead of the output?

Now, if we do that, we get something called a contravariant functor.

Now this is something a arrays can't do.

Now, for something to be a contravariant functor, we have to define a function that's called contra map, and we'll take a look at how that works.

So we start with our base function, and from this time it goes from B to C.

And then we get our transform function.

Now, if we're modifying the input, that means our transform function has to return something of type B, and at the end we want something that takes an A and returns a C.

And as you'd expect we just smush them together.

and we get a function out at the end.

Now, if you are having trouble telling the difference between that and map, that's actually a really good sign.

That means you're following because they're very similar.

Here's map again.

Here's Contra map.

See the difference?

We just swap the composition around.

That's it.

And some of the letters change so that they go A, B, C, D.

And what does that look like in code?

it looks a lot like map, except this time that transform function, it gets the that input X first, and then we pass it to the base function.

Now, what does this mean if we're gonna use it with React components?

here's how the type diagram looks if we substitute in a React component.

And once again, let's think about what happens if we change that A this time to props.

Now you guessed it.

We get back a new reusable component at the end.

So what could we do with that?

with that, we can create functions that modify props, and then we contra map that with components and we get new reusable components.

So here I've, let's, let's give a real example here.

So let's suppose that in my corner of the application where I'm working, most of the buttons default to blue instead of the gray that they happen to come as the standard default.

So what we could do is create a function that sets the … that appearance, which is appearance primary, gives us the blue button.

We could set that as the default.

We use contramap to apply that to a button and also to a badge component.

And we get new, components that have that set for us as a default, and it looks like this.

But because of the order in which we did that spread rest operation, then I can still pass through an appearance default and it goes back to the standard gray.

And of course we could flip that ordering around.

And instead of setting defaults, we could hard code props.

So let's imagine we've got some form component, and we've got some part of our, application, our feature that we don't want released yet.

So we're just gonna disable all of it.

What we can do is we can create an alwaysDisabled function, it takes some props and what it does is it just hard codes isDisabled to true.

It doesn't matter what you pass into that one isDisabled is always gonna come out true at the end.

Then we use contramap, we apply that to two different components.

So we've reused this function and we get two new components that always set that disabled thing to true.

And then it doesn't matter what I pass in as isDisabled, it's just always off.

Now that's not all cuz these prop modifiers are cool.

An interesting thing about React components is that they take children as one of the props.

So we can use this to adjust elements inside our component.

So just to give an example, let's suppose that the designer on our team is a bit unhappy about the spacing inside our banner.

This is, coming from something called a, section message component.

Now what we can do is we can use contramap to create a new component that adds more spacing.

So what we do is we create a function that pulls out the children prop.

Wraps this div around it, which adds more spacing.

and then we use contramap to apply it to a component.

We get this new RoomyMessage component and then look at all that wide space.

Now, a limitation or like map, contramap, they're pretty cool.

Like you can do a lot with those.

If you think about it, like there's lots of ways you can modify, components on the input or the output, but there's one thing they can't do.

What they can't do is they can't change the output based on what we pass in as the input.

To do that, we need a new structure.

Now, the structure that will do that is an applicative functor.

Now for applicative functor, we need to define a function called AP.

And AP is interesting.

It assumes that the transform function we give it takes not one but two parameters and they're curried of course.

And going back to our diagrams, it might look like so.

We wanna wire that up with our base function.

And at the end we wanna get back something of type A to C.

So how are we gonna wire that up?

the way AP works is that it pipes that Input A to both the transform function and the base function.

And so our transform function gets both the input and the output.

And so we can change that output however we want.

Now, what does this look like in code?

this one you gotta pay a little bit more attention to, but it's not, that much.

So again, we take our transform func, our base func return a new function, it takes X and it passes that X into the transform func and base func.

And then it takes the result of base func, passes that into transform func as well, and returns all of that.

Now, what does that look like if we plug in the React component types?

it looks like this.

And once again, at the bottom we get out a new reusable component.

But what that means is our transform function has to take props and a node and return a node.

What could we do with this?

let's suppose we had a component, like maybe a text field, and when this form component is disabled, we don't just want it to go gray and non-editable.

No, we want it to disappear completely gone.

What we can do is it can create a function called hide … hideIfDisabled.

So it takes some props and it pulls out the isDisabled property.

Then it takes a node, then it looks like that isDisabled property and decides whether or not to return null or the node straight through.

And then what we can do is we can use AP to wire that up and apologies, I've got some old code in there.

Ignore the func dot.

we can wire that up with a text field component and we get a new component called a disappearing field.

And then we use that inside our application and see on the sort of top half of the code I've passed in isDisabled as false.

And then when isDisabled is true component's gone.

Now this applicative functor is pretty cool.

I'm sure you can imagine lots of other stuff you could do with it.

I want us to ponder something for a moment.

Let's look at that transform function again.

Now above that dotted line, we have the type props.

And if we give this function props, we get back a node to node function.

But what would happen if we swapped the order?

What if we gave it a node first?

that would look like this.

And so we have a function that we give a node and returns a props to node function.

As we have a function that takes a node and returns a component, so we could redo it like this.

Now there is a special kind.

This is a special kind of shape, and the algebraic structure that lets us wire up transform functions with this shape is called monad.

And the rules for monad are 1.

already has to be a functor.

We've already checked that, functions are functors.

And then we have to define a function called chain or flatmap, it depends on who you are talking to.

And this lets us wire up functions that take some parameter, some parameter and return the shape we are already dealing with.

So there is a flat map for arrays.

it takes some input and returns, and it expects the transform function to return another array.

Now for functions, it would be a function that takes some input and returns another function.

So if we look at the wiring diagram again, we've just switched the B and the A for that transform function.

and that means that, I've shifted the position of where the red thing was.

but otherwise it's pretty similar to AP.

But with React components, check out the transform function now.

It takes a node and returns props to node, which is another component.

Sorry.

Now what could we do with that?

mostly the same things we can do with AP.

So why bother telling you about it?

this chain function has an interesting feature.

The way the types line up mean that we can build a chain or a pipeline of functions that return components and we can use those to apply successive transformations.

So I'm gonna run through this pretty quickly, but bear with me.

What we're gonna do is we're gonna try and make a modal dialogue.

Now in Atlas Kit you have to build your own out of the pieces that Atlas Kit gives you.

So we're gonna grab a modal and a modal transition out of the Atlas kit.

and then we're gonna write a function called showIfOpen, which takes a node called and some props and it pulls out, isOpen from that.

And then it decides whether or not to pass through inner or return not, which should seem a little bit familiar.

Then we're gonna create another helper function.

This one's called with modal transmission, and all it does is just wrap some element or node in the modal transition, which is the thing that controls the in and out sort of animation.

And then finally, we're gonna create this wrapInModal function.

It has that same shape where it takes a node and then some props, and then returns a node.

And this time it's pulling out the props that are just relevant to the modal dialogue and just applies those and wraps that around the whole thing.

Now, bear with me.

We're gonna also define something called compose.

Now, what compose lets us do is apply successive map transformations all in one go.

So we're gonna drop our pretense that we can't have multiple parameters.

this function just takes as many parameters as we want and it maps them all together.

we just use a reduce to make that happen in the right order.

So once we've got that, we can use compose to build a function called modalify.

Now what modalify does is it composes together all those functions that we just defined, but using chain to line them up.

And then, because the last one only had one input parameter, we map and we get up, we get this new function called modalify, which will stick anything we want inside a modal.

And so we could call modalify on section message and we get a popupSectionMessage.

In our application, we can pull in some state using some hooks.

We wire things up and notice how in popupSectionMessage, it has props for both the modal and the section message.

And that pipeline we had just pulls out the relevant ones in the spot, right spot, and they just go to the right place.

I think it's magical.

And just to prove it, it works.

Here it in a screenshot.

Sorry, I don't have live, code, but I didn't wanna risk it.

But it does work.

And I have code on my blog and I have code samples that I can show you.

now after all that, you may be decidedly underwhelmed because I haven't shown a single thing here that you couldn't already do with JSX.

And in fact, you may even be thinking, this is just higher order components.

And indeed people have been talking about higher order components in React for ages.

Where do you think they got the name from?

My point here wasn't to show you anything new.

As I said, there's nothing here you couldn't do with JSX, but the point is that looking at functions and React components through this lens opens up different ways of thinking.

Like I bet you would never have thought of creating a composition pipeline for React components.

And you sometimes come to interesting conclusions.

And there's another thing.

Like today, we started off talking about how arrays are functors.

So they have that map operation.

They also happen to have a flatmap operation.

and they have other methods that have interesting names too.

And they share some of these algebraic structures with functions.

So arrays and … and functions, they're just one or two instances of a whole myriad of data structures that implement algebraic structures.

And once you see this pattern, you start seeing these everywhere along with different ways that you can reuse code.

You can do things differently, you can apply automatic performance improvements.

and like I said, it will change the way code forever.

Now, if I've at all interested you in algebraic structures, I've just released a book just last week.

it's on sale.

It's a discounted launch price until the 9th of December.

So get in quick.

and it looks like this, it is real, I assure.

but even if you don't wanna buy a book, oh, sorry, to those who are trying to keep photos, you can grab a, a JavaScript array methods cheat sheet for free simply by signing up to my mailing list.

and I promise I won't be offended if you immediately unsubscribe.

So the URL for that one is jrsinclair.com/array-methods-cheatsheet.

And for those of you who still wanted to take photos, there are QR codes for those.

and you can follow me on either mastodon or Twitter.

I'm also on LinkedIn.

and with that I'll stop lettering, rabbiting on, let you, gimme some questions or get on with the rest of the conference.

Thanks.

all