The joy of recursion, immutable data, and pure functions: Making mazes with JavaScript

All right, let's get started.

So I'm here today to talk about, the joy of recursion immutable data and pure functions.

And we're gonna be looking at that through the lens of making mazes with JavaScript.

Now, as Ben hinted at, there's a bit of an elephant in the room that we've gotta address, and that is like, why the heck am I here at a professional web development conference talking about mazes?

Because, normally I try to be really practical when I'm writing or I'm speaking, I am trying to give people tools that they can use to make their dev lives better.

So I try to talk about things like processing JSON data or building DOM elements because those are things that you're doing every single day, right?

But mazes, they're not, so practical, right?

You're not gonna build a maze in most of your web apps, unless you're in game development.

That is.

And.

In that sense, knowing how to build a maze is essentially useless.

You're never gonna use that, right?

So why am I here?

Why bother telling you about something you're never gonna use?

And the nice thing about mazes is that they're not too big a problem and not too small a problem.

So an issue that I often have is that people come to me and they say, James, you talk about this stuff all the time.

Where's the real world example?

Where's the, thing that's in production that you can point to and say, this is it.

And.

The trouble with that is that real world examples, have all kinds of edge cases.

So in the real world, you've gotta deal with errors, you've gotta deal with the network dropping out, you've gotta deal with accessibility, you've gotta deal with input, validation, and none of these things might have anything to do with this concept that you're trying to teach or, understand.

And so they get in the way they distract from what you're trying to do.

But mazes on the other hand, they're just complex enough to be interesting and we don't have to deal with a lot of those heinous edge cases that you wanna deal with.

Also, it's not a do list, so that's a good one.

So today we're gonna look at, immutable data, and we're gonna look at recursion through the lens of, building some mazes.

So let's go.

How do we build a maze?

We start with a grid.

So this one is a four by four grid.

It has 16 rooms, and there are walls between each room.

And so we're gonna start by picking a room at random.

Now I pick one in the middle, but it can be any of the rooms in the grid.

And what we do from there is we make a list.

So we're gonna list all, the adjoining rooms, north, south, east, and west, so long as they're not already connected to another room.

Now, because this is a starting grid, none of them are connected yet.

We haven't, haven't put any doors in.

So we have all four directions.

Then what we do is we pick one of those directions at random, and what we do is we punch a hole in the wall, put in a door, and those two rooms are now connected.

And so you can see that wall's now gone and then we start the process again.

So this time, we are not listing the one to the south because we've already connected that.

We've only got the east and west 'cause the north is out bounds.

So we pick one of those at random.

And we keep connecting rooms.

This time there's only one direction we can go, so we just go south and we keep doing this and repeating this, process until we eventually we'll get to a point where we can't go any further.

And that's because we've run out of, adjoining rooms, that are unconnected.

So when we get to this spot, what we do is we just go back a step, and then we start the process again.

And eventually we keep doing this until there are no more unconnected rooms left, and we, add an entry and exit and we have a maze.

Now doing it this way has an interesting property in that there's always exactly one path between any two points in the maze.

So if we choose the entry, and the exit to be the top left and the bottom then there's exactly one path, no loops, is another way of saying that.

So let's see if we can, put that in words to come up with an algorithm.

So what we do is we start with a grid of unconnected rooms, and a randomly selected room from that grid.

We make a list of rooms that are adjacent to the current room, not yet connected to another room.

Sorry, this is really wordy.

If this list is empty, then we go back one room and we repeat from step two.

Otherwise we finish.

If we're back at the start.

Then, otherwise we pick one of those rooms in the list, at random, and we connect it and then we move, into this new room.

And then we start the whole process again.

So that's our maze algorithm that we're gonna try and turn into code.

So that's what we're gonna be doing for the most of the rest of this talk.

Not the whole thing.

We're gonna turn that algorithm into code.

But before we do that, we are gonna make life a little bit easier for ourselves by, creating our own immutable data structure from scratch.

In case you're wondering, immutable just means it doesn't change.

That's, all the word means.

You can't modify it once you've created it.

So what we're gonna do is we're gonna create a helper class.

We're gonna call it point, and all it does is, take an X value and a Y value, and, in, its constructor, assigns those to properties and we're done now.

This is rather boring and obvious so far.

And it's not immutable at all.

That's just a plain old JavaScript class.

So what we're gonna do is we are going to, take this step of hiding this away.

So we're not gonna export this.

It's gonna live in its own file.

We're gonna define the class, but we're not gonna export that.

And instead what we're gonna do is we're gonna create a constructor function, called Point with a lowercase p and we'll export that.

And, the basic idea might look something like this.

So I apologize for the contrast.

All this is doing is creating a new point, and returning it, which is still a bit useless, but what we're gonna do is we are going to memoize this function.

So what's gonna happen is that we're gonna have.

We're gonna create a cache of points.

So when a new request comes in, we look in this cache, see, have we seen this before?

And if we have, we return the one we already created.

So our cache might look something like this.

It's called allPoints, and it's just a plain old JavaScript map.

And then what we do is we create our memoized function.

So here what we do is we start by creating, turning that XY pair into a string.

We use that string to look up in our all points cache, have we seen this before?

And if we have, will we return that, one that we've already created?

Then if we haven't found this one before, we create a new point, we return that.

And or, and before we do that, we shove it in the cache.

Now, one final step, before we do, we go on, is we're gonna freeze the object when we create it.

So that means that the JavaScript runtime will say, Hey, if anybody tries to, modify the X coordinate or the Y coordinate, it's just gonna stop 'em and say, no, can't do that.

So we now have, a way to create immutable point objects.

And you might be wondering, why bother doing that?

It's pointless when you can just create a plain old JavaScript object which has an X and a Y and you're done, right?

No, no code needed for that.

So the reason we are building a special class like this is because it lets me do something that objects can't, and that is compare them with triple equals.

Here's an example.

If I create two objects, one has the values, X three and Y five, and then I create another one called object B, which has X three and Y five.

And I try to compare them with equals.

It's gonna return false.

Now the reason it's doing that is because object A and object B pointing to two different locations in memory.

'Cause I could change one and, it would be different, right?

Whereas with our point function, 'cause we memoized it point A and point B are pointing to two different lo… to the same location in memory.

And so when I compare them with triple equals JavaScript goes, is this the same location in memory?

Yes, it is.

And we get true.

Which is useful.

Now you might be saying, why is that useful?

What we can do is now that we've created this, memoized, immutable, object, we can use that with other kinds of data structures.

So for example, I can use it with a map.

Now for the rest of this talk, I'm mostly gonna be working with the map, library, the map data structure from the immutableJS library.

It's a venerable, old FP immutable data library that's been around for a long time, and it just, works very similarly to the plain old JavaScript map.

It just, makes the immutable stuff a little bit easier.

So here's an example.

If we were to use plain odd JavaScript objects and we put them in a map, we end up with two entries, even though the values are the same, which is not what we want.

We, we want is the second version where we use point, because those are the same key.

Then the second one overrides the first, and it actually works the way you'd expect.

Now, why is this important?

It's because we, are coding an algorithm, right?

And the key to getting a, a good performing algorithm is to make sure you choose the right data structure.

So we are gonna use a map in ours and we're gonna be able to use, points as keys.

So let's go into writing our algorithm.

We're gonna go over it one more time, just quickly.

So we start with the grid and the randomly selected room.

We make a list of the ones around the four, four points that are not yet connected.

If it's empty, we go back.

Otherwise we pick one at random and we connect it and then we move to the new room and we repeat from step two.

So let's dive in and let's try and tackle step one.

So what we're doing is we're setting up, the initial, state for our algorithm.

The two main things we need are a grid of unconnected rooms and a random room to start in.

So let's, start by building that out.

And the first thing is we start with that grid.

And for now we're gonna assume that we're only building square mazes.

Let's just make things a little bit simpler, and we're gonna do a little bit of math, to build out our initial grid.

This is it.

We just know that if we have a, grid with, size n then there's n squared rooms in that grid.

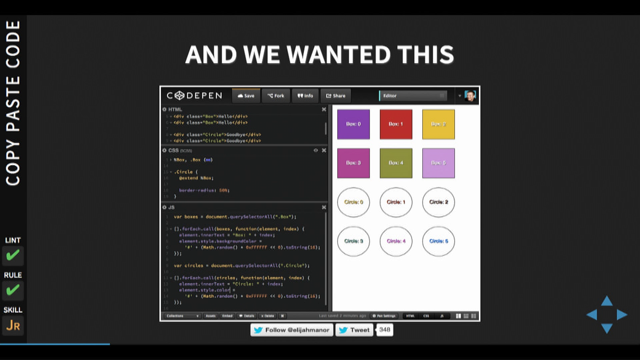
And then what we're gonna do is we're gonna build our data structure, and all that's gonna be is a map structure.

And the keys are gonna be points, and then the, values will be a list of points.

So an array of point objects, that just list the doors to other rooms.

So let's build that out.

Here we have, I'm importing the map and list from immutable.

And then I, create an empty array with n squared entries.

And then what we do is we map over that.

And so we create a list of pairs and the, left side of the pair is a point x value is I mod, Y value is I divided by n.

list because when we start, none of the rooms are connected to any other rooms.

And all we do is we pass that array into the map constructor, and we've got our initial grid.

Yeah.

Then the other thing we need for the initial state of our algorithm is a random room to start in.

Now I've said that we're gonna be working with pure functions today.

And this is a little bit of a challenge, right?

Because, normally your go-to would be math random.

But it gives you a different result every single time you run it.

And so by definition, that is not a pure function.

So what we're gonna do is gonna quickly whip up our own pseudo random number generator on the fly to sidestep this problem.

So here's what it looks like.

Now, this, incidentally is, the, method, the C language uses to, generate random numbers under the hood, but you probably never see it.

So all it's doing is it's taking in a, an integer we have, which we call seed, and it multiplies some prime numbers together, adds another, offset to that, and then mods it with, a sort of m which, reduces the scope of how big those, numbers get so they don't get outta hand.

And we get another random, another integer that's seemingly unconnected to the seed that we started with.

Now what we can do with that is we take the output of the previous one.

So let's we pass a seed into random in, we get back another number, pass that into random in again, and we go back another number.

And if we keep doing that, we can get a whole sequence of pseudo random numbers.

But if we start with the same seed, we always get the same sequence, even though they appear to be random and unconnected.

So we now have a way to generate random integers, but you normally, most of the time we're gonna want a, random number in a range.

So we're gonna want something between zero and some max number, right?

So what we're gonna do is create another helper function.

All this one does is, limits, the size by doing mod n. But it's also gonna pass us back another pseudo random number so we can use that as the next seed for generating our next round number.

And so with that in place, we now have everything we need to set up the initial state.

So we create the grid like we did before, we call random in range, to get, pick one of those rooms at random.

We look it up in the list that we just created.

And then we have a room, a grid, and a, random number C that we can pass on for the initial state of our algorithm.

Now, sorry, that's a bit boring, but.

We've got it.

We've got, the initial state, we're ready to go.

So we're ready to code our actual algorithm.

I'm gonna do this using Recursion.

Now I'm gonna take a little sidebar here.

Recursion has a bit of a, bad reputation as being scary.

Now often people think recursion is scary because it's easy to get into a state where you get into some kind of infinite recursion, right?

It is just gonna go off and it's gonna explode and it's never gonna stop.

That's fair.

I get that.

But I would ask you, I would argue that it's just as easy to get yourself into a situation where you have an infinite loop, right?

It's scary because it might never terminate, except that you don't do that.

You don't do that because you've probably either intuited or learned or been taught, some rules for writing safe loops.

Those rules are you use, pay attention to the state that you're changing.

And you always know the exit condition.

Now that second one's built into kind of the data, the structures of, the language to, to ensure that.

But the first one, you have to take care of yourself if, especially in a wild loop.

So if I'm doing something that counts to 10 or does things 10 times, we make sure that we always decrement that counter as we go through the loop, and make darn sure we do that every single time around the loop.

And we also make sure we know what that exit condition is.

So in this case, it keeps going while I is greater than zero.

So when we're writing recursive algorithms, we pay attention to the same things except they live in different locations because we're dealing in plain functions, not, a built-in structure in, the language.

So when you're writing, pure functions, as recursive functions, then the state goes in function parameters.

So if you need more bits of state to update as you're going through your algorithm, then you need more function parameters or you gotta shove everything to a big object.

And the other thing we do is we check our exit conditions as early as possible.

Now sometimes you need to do some calculations to, to check what that is, but generally we try and make sure we know what the exit condition is and we check it as soon as we can.

So let's have a think about this.

For our maze algorithm.

What's the state, that we're setting up?

So we have the room that we're considering, so we've gotta make a list of, we, each step, we're going to a particular room and looking at that one at a time.

We have the maze that we've built so far.

And one final thing that you might not have thought of is, the random seed.

We've gotta keep passing that around so that we can get new pseudo random numbers.

But if we know that we know enough to create the function signature for our recursive function, it just has a room that made so far and the pseudo random number generator, seed.

So let's get into the, second step, which is to make a list of adjacent rooms not yet connected to another room.

Now, one of the advantages of, doing things with immutable data is that constants actually make sense.

So I can create a list of points for north, south, and west.

And those are actually useful.

They're gonna be, they're never gonna change.

People can't modify them.

They're always gonna be exactly what I expect them to be and to.

Just make things a little bit easier.

I'm gonna write a function that adds two points together.

All that does is add, the X values and the Y values.

It's not terribly hard to understand.

And so with those two things, we can write our code for creating, a list of adjacent points.

Now, the way this works is we create an array of North South, East and West, a map over that with addPoint.

Now, because they were all unit one, then we get the list of, adjacent rooms in all four directions.

And then what we do is we have a look and say, is this in our map already?

See, our map has every single point, And so if it's not in the map, it must be out bounds.

And it will return undefined and it will, cast a false.

And so it'll be filtered out.

And we also check the size.

So if it's there, then it'll be an empty, it'll be a list.

And if it's an empty list, we keep it.

If it's got any entries at all, then it's already connected.

And so we, filter it out.

So that's our way of getting a list of connected, adjacent, adjacent rooms that are unconnected.

And we can put that into our main function and we are making progress on our algorithm.

But you might be thinking, what about the exiting condition?

James, you said you want to check that as early as possible?

It might be that when we create this list of adjacent rooms that are unconnected, there might not be any in there.

And so at that point, we're supposed to go back one room.

And the way we do that is by returning, that's gonna be our exit condition for the whole of this algorithm.

Because what'll happen is we go back, when we return, we go back and we'll be able to look at the previous room.

Now we're gonna figure out what that return value is in just a moment.

But for now, we know what our exit condition is.

Next, we're gonna pick one of the rooms at random, and we're gonna connect it.

Now that's easy because we've got our random number generator.

So we just call random in range.

We pass at the seed and the length of the candidates list, and we grab one of those out.

We know what room we're gonna go to.

And we then can connect some rooms, by updating our map.

Now this looks a bit, heinous, but all it's doing is grabbing the two lists, one for the current room, one for the previous room, pushing an entry onto it, and then pushing, updating the map, with those two.

Now, 'cause it's immutable, we can't just update them in place.

We have to grab them out and then shove them back in and we get a new map with the updated maze.

And then what we do is we call our recursive function.

It's a, we call build maze again with the new room, the updated, maze and a random number seed.

And we get back something that we haven't yet figured out.

But we, go off and it's gonna continue making all these, interesting windy corridors.

So we're gonna create a bunch of rooms that branch off this one.

Now, at some point it's gonna get to a point where there's no more rooms to connect.

It's get this, that, that list is empty and then it's gonna come back.

But what might happen there is there still might be unconnected rooms attached to this room that we are still considering.

And so we wanna check those to say, okay, can we build some branches off there?

And so we do that by making yet another, random call.

Sorry, another recursive call now.

At that point we need to know, what's the state now?

'cause it's gone off and it's changed, it's connected rooms, it's done a bunch of stuff.

We know what room we are in, but we dunno what the new maze looks like.

We need the updated maze.

And we will also need another random seed because, we will have generated a bunch of other ones while we've doing these recursive calls.

So we need to back another random seat so that we can keep on generating random numbers.

So that gives us enough information to work out what the return value should be from that, that call we just made.

So instead of some value we haven't figured out yet.

It is gonna be the new maze and the seed, and we can pass that into the next call.

So we're gonna do the current room, new maze, new seed, and we can update our return value and.

That's it.

That's all the recursive algorithm and it is just, sorry.

Okay.

24 lines, with a little bit of commenting and a few helper functions here and there, but not super complicated.

Then we wire that all together.

We just do a function that calls our initial state builder.

Passes that into build maze, grabs the maze out, returns it.

And that's it.

That's, our maze building algorithm.

Now let's see if it works.

So this here is a demo running that code, that exact code that you saw.

So we can change the size.

Let's make a little bit smaller.

And then if I use this seed, then I can just change this number and every single time I get a new maze.

And the neat thing about this is, because I've used immutable data and pure functions, if I know what the seed is and I find a maze that I particularly like, then I just have to note down that seed and I can always get back that same maze again.

Now, so far all we've done is, sorry, I just need to lose focus.

All we've done is talk about generating a map object, in memory.

We haven't really talked about, rendering, but the beauty of the web platform is that there are lots and lots of options for how we might render things.

For example, I could render this out as a string.

I just adjust that there now, 'cause of the shape of the characters, it's it looks a bit elongated, but it is still actually a square maze.

We could also do what I've been doing for most of this presentation, which is render them as SVGs.

The trouble with those things is that they're not terribly accessible if you are using an assisted device.

So one thing I thought we should consider is, could we build an accessible maze?

And there is a way to do that.

What we could do is we could make a list.

We could list every single room.

If it was a four by four maze, we'd have 16 list entries.

And let's face it, it's a bit dull.

It's just got coordinates and then some doors.

If we render it out, it looks like that, boring as heck, but.

What if we grabbed that list of, doors and we added a sub list.

So if there's a door to the south, we put a list that out, then we could maybe link them with some IDs.

Then we've got a link to another list item, and then we could give it a tab index of zero.

And that would allow us to give us focus.

And suddenly you can now, go through the maze using links, right?

So if we render that out.

It looks like that and still boring as heck.

This is super dull.

But what if this got me thinking maybe we could add some CSS to this, so I'm not gonna go through all the css, but what if we hid everything except the first entry or whichever one has focus.

Then we're just showing one, maze room at a time.

And maybe we could also give it maybe a background, maybe some, border images.

And maybe we could absolutely position those links so that if there's a, room to the west, we put a link on the right.

And if there's one to the north, we put it at the top.

And if we keep doing that, we end up with something that looks like this.

So it just puts a, little bit of, open source pixel light on there, and then I can click on this and then I go to the next room.

And if I keep going through, eventually this is a bit, tedious, but eventually I get to the point where I find exit door.

Now I dunno, it doesn't take much imagination to say, oh, you've got the beginnings of some kind of text adventure there.

You could put in some, random objects.

You could make things happen when you get to the, final room.

And that's all been done, with zero JavaScript, other than just generating a maze .

I'll just refocus.

So what have we done?

We have gone through and we've looked at how we might generate mazes using immutable data, pure functions, and, what else did we do?

We did recursion, which is also fun.

And you might worry well, so what, is this the, a most performant way to create a maze?

And I would say, no, it's not.

So is it then the most memory efficient way to create a maze?

And the answer is still no.

So why am I here talking to you about mazes?

And I'm gonna give you two reasons.

The first is when you look at a, use, use tools like, immutability and, pure functions and, the recursion.

It forces you to look at the problem from a different angle.

So you saw when we looked at the rendering of the maze from the accessible accessibility standpoint, suddenly, with a little bit of, creative thinking, we came up with something that was the beginnings of a text adventure game, right?

It forces looking at things differently, helped us come up with creative new ideas.

Now, I would argue that the same thing happens when you're using these functional programming techniques.

When you look at the, problem from different lens, I find at least a lot of the time I come up with more elegant solutions because it forces me to understand the problem better.

Now, it doesn't happen every time, and sometimes you might choose not to do it that way because there's performance considerations or other things that you need, to take into account, but you always end up understanding the problem better.

Now the second reason though is because it's fun, right?

I call this talk the joy of immutable data and recursion and pure functions.

And sometimes it's just fun to explore an idea and see where it takes you.

And sometimes it's fun to create a maze just for the heck of it, 'cause it's fun.

And personally, I think with all that's going on in the world, that we could all use a bit more fun and a little bit more joy in our lives.

So that's where I'll leave you.

If you want to, find more of this stuff, I have a website, jrsinclair.com.

You can find me on the, on the mastodons or the, blue skies.

I hear that's where all the kids are these days.

And if you are really interested in this kind of stuff.

I have a book which is, called The Skeptics Guide to Functional Programming with JavaScript, and you can find that at jrsinclair.com/skeptics-guide.

Thank you very much.